■今月は不思議な三角形の問題です。
この問題をパズカルの三角形！と呼ぶことにしましょう。
実は、不思議でも何でもなく、一定の規則で作ったものなのですが…。
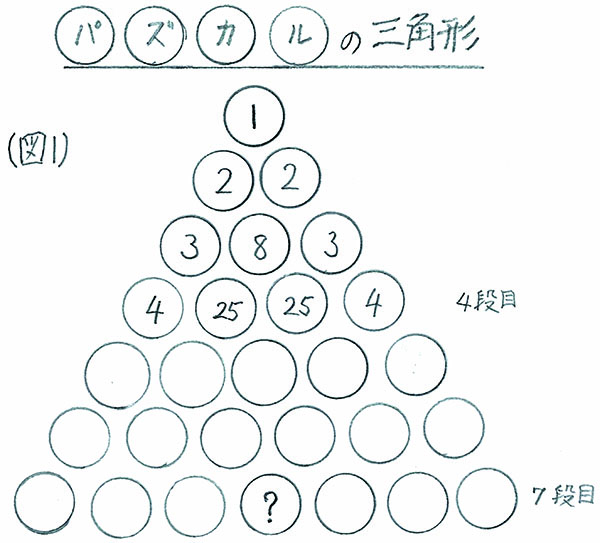
〈図1〉のような数の三角形を考え、一定のルールのもとに4段目まで求めてあります。
では、このまま続けて7段目まで計算をして、「？」のところの数を求めてみましょう。
【出題:東原 正二郎】
応募方法：はがき、FAX、メールのいずれか
記載内容：住所、電話番号、氏名、年齢、1月号の解答（発表の際、匿名をご希望の方はお書きください。その際、仮名を決めてください）。
応募締切り：2023年1月31日必着
はがきの宛先：339-0053 岩槻区城町2-11-48 ひなまちデザイン奥山（宛）
FAX：048-758-0911
メールアドレス：tamezou@kyf.biglobe.ne.jp
◎11月号の正解例と説明、正解者の発表
■最短のルートとその長さの問題の正解例と説明
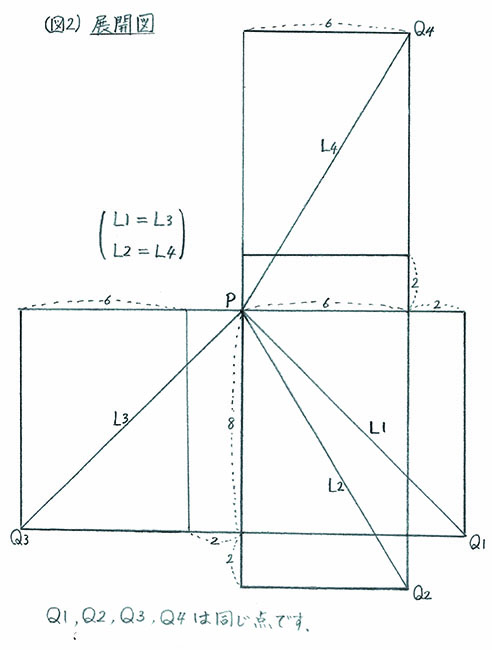
① 最短のルートは、箱の展開図を使って考えてみましょう。
〈図2〉で最短になりそうな経路は2種類あり、それぞれをL1(=L3)、L2(=L4)とします。
L2は縦10cm,横6cmの長方形の対角線になり、計算ではピタゴラスの定理により√10の2乗+6の2乗=√136(cm) =2√34(cm)展開図で測ってみると、約11.7cmとなります。
また、L1は、一辺が8cmの正方形の対角線になります。
縦横の長さを足して、同じ長さとなる長方形では、対角線が最短になる場合が、正方形のときです。
L1の対角線の長さを計算してみると、ピタゴラスの定理より√8の2乗+8の2乗=√128(cm)=8√2(cm)また、展開図で測ってみると、約11.3cmとなります。
よって、最短のルートは、L1(=L3)となり、その長さは8√2cm (近似値、計測値は約11.3cm)となります。
今回の応募者は19名で、14名の方が正解でした。
厳正な抽選で10名の方に、岩槻の関根製菓さんの協賛もあり、同店で使える菓子引換券が届けられます。
以下の方々です。
浜田真大さん、坂主明子さん、木暮耕久さん、さいたま市北区匿名さん、佐藤麻衣子さん、和田文恵さん、早川謹弘さん、小原武道さん、中嶋明子さん、どんどんさん
残念ながら、抽選で外れましたが、以下の4名方々も正解でした。
ピロ過ぎた原拍さん、関口等さん、いくらさん、ぴぴさん。
関連記事
コメント
この記事へのトラックバックはありません。
インフォメーション
-
2024-7-13
睡眠不足がもたらす健康リスクとは？⑥
睡眠改善のためのヒントとアドバイス ストレス管理と睡眠の関係 ・ストレスがたまると、睡眠不足の… -
2024-7-13
支援団体に 自動車税一千万が課税
[caption id="attachment_22457" align="alignleft" w… -
2024-7-13
伝えて槻丸 №12 第84回 たかみや えみこ
【中古】 秘伝4コママンガの描き方 今日からキミもプロ作家！！ / ドラクエ…
『らうんじ』からの募集・告知
-
2024/7/13
知ってましたか 玄奘三蔵法師と岩槻の繋がり 「武州岩槻 玄奘塔ものがたり」唐朝（とうちょう） 唐の朝廷。 唐の時代 名君（めいくん） 国家を 統制することに すぐ… -
2024/7/13
ジャズと教育 凱旋講演会！[caption id="attachment_22317" align="alignright" … -
2024/7/13
縄文落雁 ぷくみ 産学官連携により開発[caption id="attachment_22308" align="alignright" … -
2024/7/13
岩槻の市民交流カフェ（第5回）地域の疑問やあなたのアイデアを聞かせて下さい。 独自の文化や観光の魅力をたくさん持っている岩槻です… -
2024/7/13
郷土資料館の体験講座だれでもできる簡単なおもちゃづくり（材料費等無料） 【日時】①7月20日（土）②7月27日（土）③…
この記事へのコメントはありません。