■最短のルートを探そう！
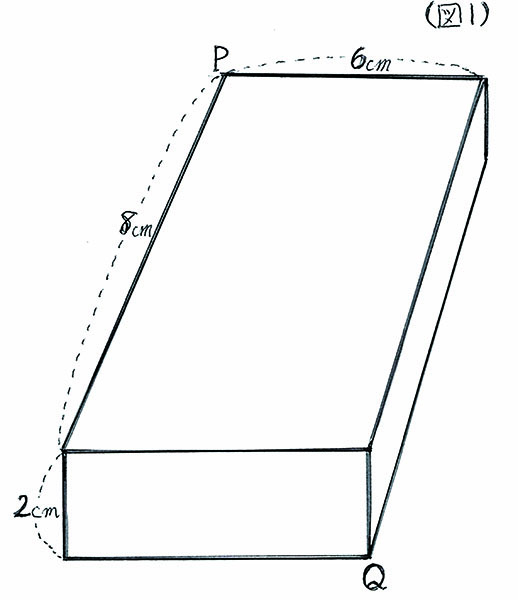
図1のような木の箱があります。
その箱は縦8cm、横6cm、高さ2cmの直方体です。
頂点Pから、頂点Qまでの最短のルート(箱の表面を通る)を見つけ、説明をつけてその長さ（上から3桁の概数でもいいです）を求めてみましょう。
【出題＝東原正二郎】
応募方法：はがき、FAX、メールのいずれか
記載内容：郵便番号、住所、電話番号、氏名、年齢、11月号の解答
［発表の際、匿名(仮名)をご希望の方はお書きください]
応募締切り：11月30日必着
はがきの宛先：339-0053 岩槻区城町2-11-48 ひなまちデザイン奥山 (宛)
FAX：048-758-0911
メールアドレス：tamezou@kyf.biglobe.ne.jp
◎9月号の正解例と説明、正解者の発表
■平面の分割の問題の正解例
まず解くにあたって、問題文中にある通り条件が①、②と同様に考えて、とありますので、無限にあると言うのは当たりません。
③の解答は次のようになります。
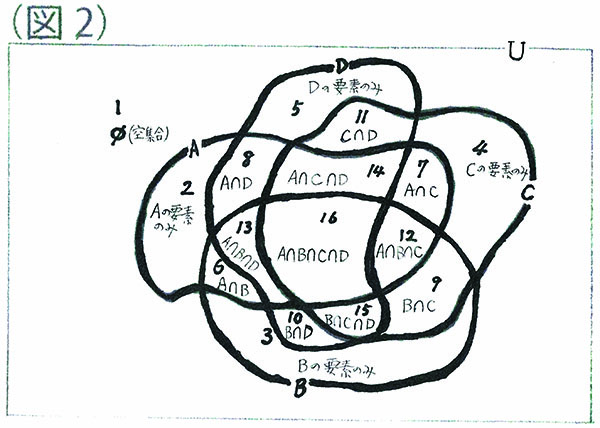
4つの閉じた曲線の集合をそれぞれ、A、B、C、Dとすると、
ø（空集合:ベン図の外側）が１つ、
A、B、C、D の要素のみの集合が、4つ、
A ∩ B、A ∩ C、A ∩ D、B ∩ C、B ∩ D、C ∩ Dで、6つ、
A ∩ B ∩ C、A ∩ B ∩ D、 A ∩ C ∩ D、B ∩ C ∩ Dで、4つ、
A ∩ B ∩ C ∩ Dが、１つ、
合計で最大16個の空間が考えられることになります。
それを図示すると、図2のようになります。
ただし、ベン図のA、 B、 C、 Dの集合を円で描くと、14通りしか表現できませんね。
今回は応募者が16名でしたが、正解者は、以下の3名の方でした。
K I C太郎さん、武田明子さん、ピロ過ぎたげんぱくさん
岩槻の関根製菓さんの協賛もあり、正解者には同店で使える菓子引換券が届けられます。
コメント
この記事へのトラックバックはありません。
インフォメーション
-
2024-7-13
睡眠不足がもたらす健康リスクとは？⑥
睡眠改善のためのヒントとアドバイス ストレス管理と睡眠の関係 ・ストレスがたまると、睡眠不足の… -
2024-7-13
支援団体に 自動車税一千万が課税
[caption id="attachment_22457" align="alignleft" w… -
2024-7-13
伝えて槻丸 №12 第84回 たかみや えみこ
【中古】 秘伝4コママンガの描き方 今日からキミもプロ作家！！ / ドラクエ…
『らうんじ』からの募集・告知
-
2024/7/13
知ってましたか 玄奘三蔵法師と岩槻の繋がり 「武州岩槻 玄奘塔ものがたり」唐朝（とうちょう） 唐の朝廷。 唐の時代 名君（めいくん） 国家を 統制することに すぐ… -
2024/7/13
ジャズと教育 凱旋講演会！[caption id="attachment_22317" align="alignright" … -
2024/7/13
縄文落雁 ぷくみ 産学官連携により開発[caption id="attachment_22308" align="alignright" … -
2024/7/13
岩槻の市民交流カフェ（第5回）地域の疑問やあなたのアイデアを聞かせて下さい。 独自の文化や観光の魅力をたくさん持っている岩槻です… -
2024/7/13
郷土資料館の体験講座だれでもできる簡単なおもちゃづくり（材料費等無料） 【日時】①7月20日（土）②7月27日（土）③…
この記事へのコメントはありません。